Реферат: Інформаційні технології вирішення задач векторної оптимізації

ІНФОРМАЦІЙНІ ТЕХНОЛОГІЇ РОЗВ'ЯЗАННЯ ЗАДАЧ ВЕКТОРНОЇ ОПТИМІЗАЦІЇ

план:

Вступ

Принцип оптимальності Парето. Неулучшаемие (оптимальні по Парето) рішення

Принцип рівноваги Неша

Конфлікти, переговори і компроміси

Короткий огляд методів розв'язання задачі векторної оптимізації

На відміну від завдань обґрунтування рішень по скалярному критерію, результатом яких є оптимальна (з точністю до передумов і припущень моделі) стратегія, в задачах з векторним критерієм виявляється неможливо з абсолютною впевненістю стверджувати, що те чи інше рішення, дійсно (об'єктивно) оптимально. Одне з рішень може перевершувати інше за одними критеріями і поступатися йому за іншими. Сказати, яке з двох рішень в зазначених умовах об'єктивно кращий за інший, не представляється можливим. Тільки з часом буде ясно, наскільки вірним було прийняте рішення; поки ж, до реалізації рішення, особисті переваги ОПР, його досвід і інтуїція є тією основою, яка визначає здатність ЛПР передбачити наслідки прийнятого ним компромісу.

Таким чином, складність проблеми прийняття рішень по векторному критерію навіть в умовах визначеності пов'язана не стільки з обчислювальними труднощами, скільки з концептуальної обгрунтованістю вибору оптимального рішення. Неможливо строго математично довести, що обране рішення найкраще, - будь-яке рішення з числа недомініруемих, тобто неулучшаемих одночасно по всім приватним критеріям, може виявитися найкращим для конкретного ОПР в конкретних умовах. З тієї ж точки зору не має сенсу говорити про найкращий вирішенні взагалі. Це може вважатися аксіомою обґрунтування рішень за кількома критеріями.

Порівняння альтернатив по векторному критерію здійснюються за наступним правилом: будь-яка альтернатива не гірше будь-якої іншої, якщо для неї значення векторного критерію не менше переважно, ніж значення критерію іншої альтернативи, тобто:

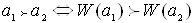
де де 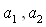- альтернативи; 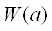- векторний критерій; - символ відносини несуворого переваги - альтернативи; - векторний критерій; - символ відносини несуворого переваги.

Припустимо, що множинність критеріїв пов'язана з наявністю декількох сторін, зацікавлених у вирішенні проблемної ситуації. Кожна сторона прагне знайти і прийняти рішення, при якому її показник ефективності (цільова функція) був би найбільшим. Очевидно, величина показника ефективності кожного боку залежить від рішень всіх інших сторін. Тому найбільш ефективні для однієї сторони рішення не є такими для інших. У зв'язку з цим, прагнення кожного боку домагатися найбільшої ефективності прийнятих нею рішень носить конфліктний характер і саме формулювання того, яке рішення є прийнятним, хорошим чи найкращим (оптимальним), проблематична.

Розгляд складних економічних об'єктів, що характеризуються цілим спектром характеристик, призводить до необхідності введення понять локального і глобального критеріїв оптимальності. При цьому математично глобальний критерій формулюється у вигляді скалярної цільової функції, яка узагальнено виражає різноманіття цілей, або у вигляді векторної функції, що представляє собою набір несвідомих один до одного приватних цільових функцій (локальних критеріїв).

Слід зазначити, що множинність цілей розвитку економічних систем суттєво ускладнює планування, особливо якщо цілі різноспрямовані, і наближення до одним цілям видаляє систему від досягнення інших. В результаті виникає завдання їх узгодження. Метою многокритериальной або векторної оптимізації і є відшукання найкращих рішень за кількома критеріями.

Серед безлічі багатокритеріальних задач можна виділити завдання чотирьох типів:

Завдання оптимізації на множині цілей, кожна з яких повинна бути врахована при виборі оптимального рішення. Прикладом може служити завдання складання плану роботи підприємства, в якій критеріями служить ряд економічних показників;

Завдання оптимізації на множині об'єктів, якість функціонування кожного з яких оцінюється самостійним критерієм. Якщо якість функціонування кожного об'єкта оцінюється декількома критеріями (векторних критерієм), то таке завдання називається багатовекторною. Прикладом може служити завдання розподілу дефіцитного ресурсу між декількома підприємствами. Для кожного підприємства критерієм оптимальності є ступінь задоволення його потреби в ресурсі або інший показник, наприклад, величина прибутку. Для плануючого органу критерієм виступає вектор локальних пріоритетів підприємств;

Завдання оптимізації на множині умов функціонування. У завданнях такого типу заданий спектр умов, в яких доведеться працювати об'єкту, і стосовно кожного умові якість функціонування оцінюється деяким приватним критерієм;

Завдання оптимізації на безлічі етапів функціонування. Розглядається функціонування об'єктів на деякому інтервалі часу, розбитому на кілька етапів. Якість управління на кожному етапі оцінюється приватним критерієм, а на безлічі етапів - загальним векторних критерієм. Прикладом може служити розподіл квартального плану цеху по декадах. У кожній декаді необхідно забезпечити максимальне завантаження. В результаті вийде критерій максимізації завантаження в кожної декаді кварталу.

Багатокритеріальні задачі можна також класифікувати за іншими ознаками, наприклад, за варіантами оптимізації, по числу або типам критеріїв, за співвідношенням між критеріями, за рівнем структуризації, наявності фактора невизначеності і т.п.

При розробці методів рішення векторних задач доводиться вирішувати ряд специфічних проблем.

Проблема нормалізації виникає в зв'язку з тим, що локальні критерії мають, як правило, різні одиниці і масштаби виміру, і це унеможливлює їх безпосереднє порівняння. Операція приведення критеріїв до єдиного масштабу і безрозмірного вигляду називається нормуванням. Найбільш поширеним способом нормування є заміна абсолютних значень критеріїв їх відносними величинами.

Проблема вибору принципу оптимальності пов'язана з визначенням властивостей оптимального рішення і вирішенням питання - в якому сенсі оптимальне рішення вигідно відрізняється від інших.

Проблема врахування пріоритету критеріїв виникає, якщо локальні критерії мають різну значимість. Необхідно знайти математичне визначення пріоритету і ступінь його впливу на рішення задачі.

Проблема обчислення оптимуму виникає, якщо традиційні обчислювальні схеми та алгоритми непридатні для вирішення завдання векторної оптимізації.

Якісна інформація про відносну важливість критеріїв найчастіше є повідомлення про те, що якісь критерії "рівноцінні" або ж "один критерій важливіше інших". Така інформація може бути отримана в ході контрольного пред'явлення ЛПР спеціально формованих векторних оцінок і з'ясування, які з них він вважає за краще при порівнянні з іншими. При цьому пред'являються ЛПР оцінки повинні задовольняти двом спеціальним вимогам. По-перше, всі приватні компоненти таких спеціальних оцінок повинні мати загальну шкалу, тобто бути однорідними. По-друге, в пропонованих оцінках всі компоненти, крім тих, чия відносна важливість з'ясовується, повинні бути однаковими.

Для того щоб забезпечити однорідність приватних критеріїв, які, взагалі кажучи, мають різні шкали, в практиці часто використовують прості прийоми еквівалентного перетворення неоднорідних приватних критеріїв до єдиного, безрозмірного вигляду. Використовуються такі формули перетворень (як стандарт вибрано перетворення в шкалу зі значеннями з відрізка [0; 1]:

Якщо відомі еталонні значення показників 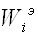(Наприклад, міжнародний стандарт), то використовується перетворення такого вигляду:

;

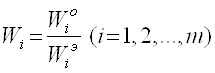Якщо відомі максимально можливі значення показників, то

;

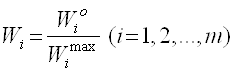Якщо відомі діапазони зміни показників, то

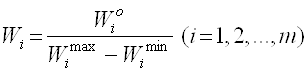
або або .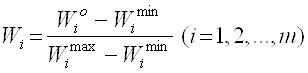

Перш ніж приступити до розгляду алгоритмів розв'язання задач векторної оптимізації, має сенс коротко зупинитися на деяких фундаментальних поняттях теорії прийняття рішень в контексті багатокритеріальних задач.

Принцип оптимальності Парето. Неулучшаемие (оптимальні по Парето) рішення

Розглянемо проблемну ситуацію, вирішення якої оцінюються за деякою сукупністю показників 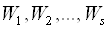(під 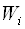може розумітися, наприклад, цільова функція, що описує будь-яку характеристику виробничого процесу, показник функціонування підприємства і т.п.). Для наочності можна представляти, що у виборі рішення беруть участь 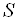сторін, кожна з яких зацікавлена в максимізації відповідного ( "свого") показника. При цьому 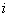-я сторона може вибрати будь-яке припустиме для неї рішення 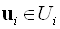. Надзвичайно важливо, що рішення, вбрання цією стороною, впливає на ефективність усіх інших. Це означає, що показник ефективності будь-якого боку залежить від сукупності допустимих рішень 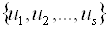усіх боків, тобто .

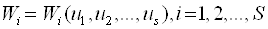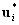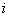Рішення Рішення боку краще її рішення , Якщо: боку краще її рішення , Якщо:

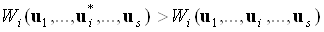На підставі вищесказаного (враховуючи наявність 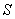сторін, самостійно вибирають свої рішення), можна сформулювати принцип одноголосності, відомий як принцип оптимальності Парето):

Якщо для всіх сторін допустимі рішення 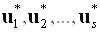переважніше рішень , То останні не будуть прийняті (одноголосно відкинуті).

Як правило, на практиці сукупність рішень виявляється неєдиним і утворює деякий безліч 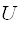рішень, оптимальних за Парето. Будь-який набір рішень з цього безлічі не може бути поліпшений відразу за всіма показниками 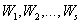. В силу цього рішення, оптимальні по Парето, називаються також неулучшаемимі. Слід зазначити, що завдання, в яких є єдина сукупність неулучшаемих рішень, зустрічаються виключно рідко. Будь-яке рішення з безлічі 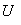є неулучшаемим. Зміною цього рішення неможливо домогтися збільшення будь-якого показника ефективності, не зменшуючи при цьому хоча б одного з решти. Вибір конкретного рішення з безлічі оптимальних по Парето може бути здійснений лише на основі компромісу на основі переговорів ЛПР всіх зацікавлених сторін.

Хоча до цих пір ми вважали, що у виборі рішення беруть участь 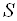різних сторін, розглянуті поняття і вся формулювання в цілому абсолютно аналогічні і в тому випадку, коли вибір рішення 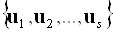здійснює одна сторона, яка керується не єдиним, а деякою сукупністю 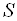показників ефективності. Ухвалення будь-якого конкретного рішення з безлічі Парето є при цьому прерогативою виключно ЛПР і здійснюється, як правило, на основі його суб'єктивних переваг.

Принцип рівноваги Неша

Нехай всі сторони вибрали рішення, оптимальні по Парето (назвемо цю ситуацію оптимальної по Парето). Відповідно до принципу оптимальності Парето, всі сторони, діючи спільно, не можуть збільшити ефективність своїх рішень. Однак будь-яка сторона, ухилившись від ситуації, оптимальної по Парето, при певних умовах може домогтися більшого значення "свого" показника ефективності. Іншими словами, ситуації, оптимальні по Парето, не володіють стійкістю по відношенню до відхилень від них будь-якої сторони. У той же час бажано, щоб жодна зі сторін, діючи поодинці, не могла збільшити ефективність обираних нею рішень. Іншими словами, необхідний пошук таких ситуацій, відхилення від яких було б невигідним ні для однієї із сторін окремо.

Існування ситуацій, які є стійкими в сенсі невигідність відхилення від них жодної зі сторін, призводить до принципу рівноваги Неша.

Ситуацію, що характеризується набором рішень 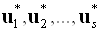, Називають рівноважною Неша, якщо для всіх 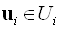має місце нерівність:

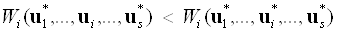Якщо прочитати ці нерівності справа наліво, то можна бачити, що заміна якого-небудь одного рішення, що входить в рівноважну ситуацію, будь-яким іншим з безлічі допустимих, зменшує відповідний показник ефективності. якщо під 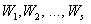Якщо прочитати ці нерівності справа наліво, то можна бачити, що заміна якого-небудь одного рішення, що входить в рівноважну ситуацію, будь-яким іншим з безлічі допустимих, зменшує відповідний показник ефективності розуміти показники ефективності сторін, то з визначення ситуації рівноваги Неша слід, що ні одна з них не зацікавлена в зміні рішення входить в ситуацію рівноваги, якщо всі інші сторони зберігають рішення, що відповідають цій ситуації.

Таким чином, якщо сторони попередньо домовляються про вибір рішень, що утворюють рівноважну ситуацію, то індивідуальне порушення цього договору невигідно порушнику. Відзначимо деякі особливості рівноважних ситуацій:

Ситуація рівноваги може виявитися не єдиною.

Ситуації рівноваги часто виявляються в різному ступені кращими для різних сторін. Інакше кажучи, показники ефективності рішень сторін мають неоднакові значення в різних рівноважних ситуаціях. У зв'язку з цим якась рівноважна ситуація, вигідна для одного боку, може надаватися невигідною для інших. Тому рішення 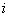Ситуації рівноваги часто виявляються в різному ступені кращими для різних сторін -й боку, відповідне будь-якої рівноважної ситуації, не слід трактувати як оптимальне для цієї сторони. Рівновага як принцип оптимальності має сенс тільки для набору рівноважних рішень усіх боків.

Ситуації рівноваги можуть збігатися або не збігатися з ситуаціями оптимальними по Парето.

Конфлікти, переговори і компроміси

Рішення сторін (учасників конфліктної ситуації) можуть бути вигідними для всіх (рішення, оптимальні по Парето), але нестійкими, або стійкими (рівноважними Неша), але не обов'язково найкращими, що характеризуються найбільшими значеннями показників ефективності. При цьому нестійкість ситуацій, оптимальних за Парето, означає, що вихід з цієї ситуації будь-якого з учасників може виявитися вигідним для нього. Стійкість рівноважної Неша ситуації означає, що індивідуальний (поодинці) вихід з неї невигідний стороні, яка наважилася на це.

Ситуації, оптимальні по Парето, еквівалентні для всієї сукупності учасників конфлікту. Тому вибір якоїсь однієї ситуації з безлічі оптимальних по Парето повинен здійснюватися шляхом проведення відповідних переговорів між сторонами і є компромісне рішення цих сторін. Але і про вибір рішень, що відповідають тим чи іншим рівноважним ситуацій, сторони повинні попередньо домовитися, так як ефективність цих рішень неоднакова для різних сторін.

Таким чином, переговорний процес, спрямований на вироблення компромісних угод, є істотним чинником вирішення конфліктних ситуацій. В ході переговорів можуть визначатися не тільки рішення, але і процедури, правила поведінки, що дозволяють відшукати рішення, прийнятні для всіх сторін.

Для забезпечення стійкості ситуацій може застосовуватися, наприклад, утворення коаліцій, що пов'язано з наступним. При виробленні угоди між сторонами про вибір рішень, відповідних рівноваги Неша, враховується позиція кожного боку. На відміну від цього Парето-оптимальні рішення визначаються спільним інтересом усіх боків. Природно, можливі проміжні випадки, коли кілька сторін об'єднуються в одну коаліцію. При цьому коаліційні результати виявляються кращими, ніж індивідуальні (інакше утворення коаліцій не мало б сенсу). Число утворених в деяких випадках коаліцій може надаватися досить великим.

Ефективним способом забезпечення стійких Парето-оптимальних угод є вироблення спеціальних процедур ведення переговорів по вибору рішень, що базуються на розширенні взаємної інформованості сторін про їх рішеннях і наміри.

Крім розширення інформованості сторін є й інші шляхи стабілізації можливих результатів, які визначаються конкретними особливостями конфліктних ситуацій. Однак наявність безлічі нерівнозначних для різних сторін варіантів ускладнює пошук компромісу, тому що кожна сторона прагне відстоювати найбільш вигідний для себе варіант. У зв'язку з цим виникають нові проблеми, які потребують вирішення. Як приклад можна привести боротьбу "за перший хід". Не виключена також можливість дезінформує дій учасників переговорів, а також небезпека зриву переговорного процесу і т.д.

Короткий огляд методів розв'язання задачі векторної оптимізації

Рішення завдання векторної оптимізації являє собою складний процес, в ході якого можуть застосовуватися різні розрахункові схеми і алгоритми. Перерахуємо деякі з найбільш уживаних:

Методи, засновані на згортання системи показників ефективності;

Методи, які використовують обмеження на критерії;

Методи цільового програмування;

Методи, засновані на знаходженні компромісного рішення;

Методи, в основі яких лежать людино-машинні процедури прийняття рішень (інтерактивне програмування).

Для ряду з перерахованих вище методів вводиться поняття функції переваги (корисності). За допомогою функції переваги проблема порівняння сукупності чисел-значень, прийнятих показниками ефективності, зводиться до порівняння чисел-значень, прийнятих функцією переваги. При цьому ЛПР вважає, що один набір значень локальних критеріїв переважніше іншого, якщо йому відповідає більше значення функції переваги. Коротко охарактеризуємо згадані методи векторної оптимізації.

А. У методах, заснованих на згортання системи показників ефективності, з локальних критеріїв формується один. Найбільш поширеним є метод лінійної комбінації локальних (приватних) критеріїв.

Нехай розглянута економічна система характеризується набором локальних критеріїв (цільових функцій) 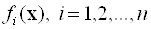і відомий вектор вагових коефіцієнтів (вектор пріоритетів) критеріїв 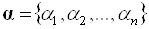, Що характеризує важливість відповідних критеріїв, причому:

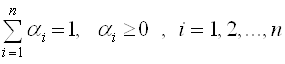У цьому випадку функція переваги 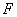вибирається у вигляді:

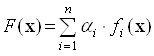(5.1)

і завдання векторної оптимізації зводиться до задачі скалярної оптимізації, розглянутої раніше. При вирішенні даного завдання враховується система функцій-обмежень для кожної з цільових функцій 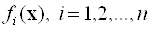і завдання векторної оптимізації зводиться до задачі скалярної оптимізації, розглянутої раніше . До недоліків даного методу можна віднести те, що рішення, оптимізує функцію переваги, може виявитися незадовільним по одному або відразу декільком приватним показниками. Це пояснюється тим, що при досягненні максимуму функції переваги неприпустимо малі значення деяких показників 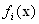компенсуються великими значеннями інших.

До цієї ж групи методів відносяться методи, в яких використовується среднестепенная функція переваги виду:

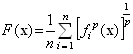де параметр .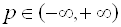

оптимальність парето векторний багатокритерійний

Б. Методи, які використовують обмеження на критерії, включають два підходи: метод ведучого критерію і метод послідовних поступок.

У методі провідного критерію все цільові функції, крім однієї, переводяться в розряд обмежень. нехай 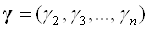- вектор, компоненти якого є нижні межі відповідних критеріїв. Тоді задача записується у вигляді:

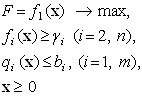
де де 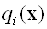- вихідна система функцій-обмежень - вихідна система функцій-обмежень. Метод провідного критерію застосовується в таких завданнях, як мінімізація повних витрат за умови виконання плану по виробництву різних видів продукції, максимізація випуску комплектних наборів при обмеженні на споживані ресурси і ряду інших.

Алгоритм методу послідовних поступок полягає в наступному:

Критерії нумеруються в порядку убування важливості;

Визначається оптимальне значення найважливішим критерієм . Особою, яка приймає рішення, встановлюється величина поступки 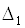за цим критерієм;

Вирішується задача за критерієм з додатковим обмеженням ;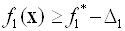

Пункти 2 і 3 повторюються послідовно для критеріїв .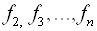

В. При вирішенні завдань методами цільового програмування передбачається наближення значення кожного критерію до певної величиною 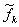, Тобто досягнення певної мети. У найзагальнішому вигляді завдання цільового програмування може бути сформульована як мінімізація сум відхилень цільових функцій (критеріїв) від цільових значень з нормованими вагами :

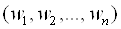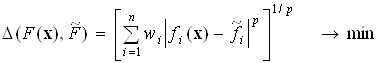, (5 , (5.2)

де де 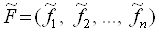- вектор цільових значень, 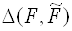- відстань (міра відхилення) між и , - вектор цільових значень, - відстань (міра відхилення) між и 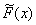, 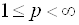. Часто (наприклад, в разі лінійного цільового програмування) вважають 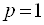. Слід зазначити, що точка 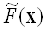, Як правило, не належить області допустимих значень, в зв'язку з чим, її іноді називають ідеальною або утопічною точкою.

Г. В методах, заснованих на знаходженні компромісного рішення, використовується принцип гарантованого результату. Завдання може бути сформульована таким чином:

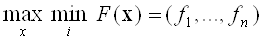. (5.3)

Даним методом можуть вирішуватися завдання з заданими пріоритетами критеріїв і багатовекторні завдання.

Д. У методах заснованих на людино-машинних процедурах (методи інтерактивного програмування) рішення задачі відбувається в інтерактивному режимі. ЛПР оцінює отримане рішення і вносить або змінює наперед задані коефіцієнти або поступки по критеріям, а також визначає напрямок оптимізації. Ця інформація служить для постановки нової задачі оптимізації та отримання проміжного рішення. Діалог триває до тих пір, поки рішення не буде задовольняти вимогам ОПР. Основною перевагою даного методу є використання знань і інтуїції ОПР, глибоко розуміє сенс завдання і здатного правильно коригувати проміжні результати в потрібному напрямку.

Відзначимо ще один важливий метод агрегування цільової функції. У деяких випадках, коли одні приватні критерії бажано збільшувати, а інші - зменшувати, може бути використана функція агрегування у вигляді відношення одних критеріїв до інших. При цьому перша група критеріїв ототожнюється з цільовим ефектом, а інша - з витратами на його досягнення. Результатом агрегування в цьому випадку виступає питома ефективність:

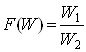де де 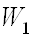- прибуток (позитивний ефект), - витрати - прибуток (позитивний ефект), 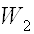- витрати. Цей метод часто називають методом "витрати - ефект".

Перейдемо до розгляду інформаційних технологій вирішення низки завдань векторної оптимізації. В процесі розгляду ми обмежимося найбільш широко використовуваними методами. Для вирішення завдань будемо використовувати процесор електронних таблиць Excel, здатний досить просто і ефективно вирішувати завдання подібного роду.

Приклад 1. Згортання системи показників ефективності.

Розглянемо наступну задачу векторної оптимізації:

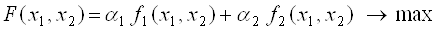де цільові функції і відповідні їм обмеження мають вигляд:

Вирішимо задачу в Excel і проаналізуємо залежність одержуваного рішення від значення коефіцієнтів .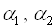

Внесемо дані на робочий лист відповідно до Рис. 5.1. Під значення змінних відведемо осередку A16: C16. В осередку A6: A8 і A10: A12 введемо формули, що визначають обмеження на значення змінних, в осередку E16 і G16 - формули для розрахунку відповідних цільових функцій, в осередок F20 - формулу для розрахунку функції 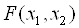Внесемо дані на робочий лист відповідно до Рис .

Надзвичайно важливим є використання в даному методі загальної для всіх функцій системи обмежень.

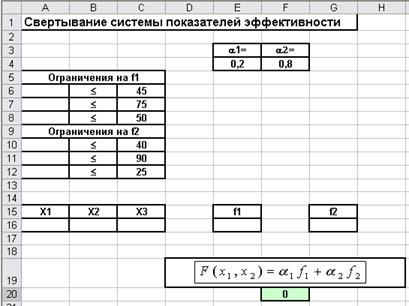
Мал. 1. Дані для вирішення прикладу 1

Викличемо Пошук рішення і задамо область зміни змінних, цільову комірку і систему обмежень стандартним чином. В результаті отримаємо відповідь: (для даних значень параметрів 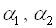Викличемо Пошук рішення і задамо область зміни змінних, цільову комірку і систему обмежень стандартним чином (Див. Рис. 1)) 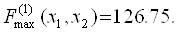Вважаючи значення параметрів рівними, наприклад, 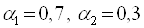отримаємо інше оптимальне значення досліджуваної функції 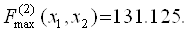Таким чином, можна зробити висновок про досить суттєвою чутливості значень даної оптимізується функції до варіацій вагових коефіцієнтів.

Приклад 2. Обмеження на критерії. Метод послідовних поступок.

Обмежимося для простоти завданням лінійної оптимізації (лінійного програмування).

Нехай необхідно вирішити задачу векторної оптимізації такого вигляду:

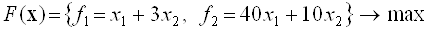
при обмеженнях:

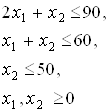
методом послідовних поступок, якщо поступка за першим критерієм становить 10% від його оптимального значення.

Рішення. Вирішимо задачу за критерієм 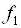, В результаті чого отримаємо . У відповідності до розділу завдання величина поступки 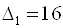. Додаткове обмеження матиме вигляд: 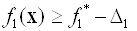, Тобто 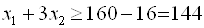. вирішуючи задачу

отрімаємо

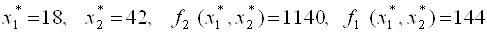Проведемо рішення задачі за допомогою Excel. Введемо дані на робочий лист відповідно до Рис.2.

Відведемо під значення змінних осередку A19 і B19, введемо формули, що визначають обмеження вихідної задачі, в осередку A13: A15; формулу для цільової функції в комірку E19, а формулу для розрахунку Відведемо під значення змінних осередку A19 і B19, введемо формули, що визначають обмеження вихідної задачі, в осередку A13: A15; формулу для цільової функції в комірку E19, а формулу для розрахунку 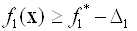в осередок H19 в осередок H19. Пошук рішення дає значення 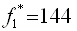. Далі, копіюємо значення з комірки E19 в клітинку С26 (використовується спеціальна вставка - тільки значення). Потім відводимо під цільову комірку E26, вводимо в неї формулу для розрахунку , А в клітинку A26 вводимо формулу = A19 + 3 * B19, що представляє собою додаткове обмеження завдання.

При вторинному запуску Пошуку рішення поряд з уже введеними на першому етапі обмеженнями вводимо ще одне додаткове обмеження A26> = 144.

В результаті розрахунку отримаємо відповідь:

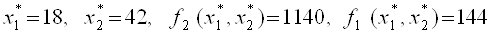Мал. 2. Дані для розв'язання задачі оптимізації за методом послідовних поступок

Приклад 3. Цільове програмування.

Провести оптимізацію вектор - функції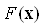

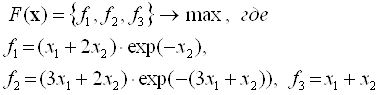
при обмеженнях:

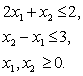
Мал. 3. Дані для вирішення прикладу 3

Рішення. Введемо дані на робочий лист відповідно до Рис.3.

Відведемо під значення змінних осередку A20 і B20; введемо формули, що визначають обмеження завдання, в осередку A16: A17; формули для розрахунку функцій 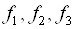в осередку E20, G20 і I20, а формулу для розрахунку 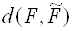- у комірку C28. Оскільки наші функції нелінійні, у вікні діалогу Параметри пошуку рішення необхідно зняти прапорець (покажчик) лінійна модель.

Далі послідовно проводимо пошук оптимальних (максимальних) значень функцій 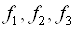(Цільовими осередками вибираємо E20, G20 і I20); після знаходження оптимальних значень кожної з функцій її максимальне значення заносимо (використовуючи спеціальну вставку) в осередку E24, G24 і I24 відповідно. Таким чином, в осередках виявляться значення: 1.0748 (E24), 0.7357 (G24), 2 (I24).

Після цього переходимо до заключного етапу. Оптимізуємо (мінімізуємо) значення цільової функції 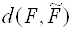(Цільова осередок С28). Пошук рішення дає для оптимального значення цільової функції значення 0,32534. При цьому в осередках E20, G20 і I20 виявляться значення функцій 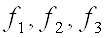, Що відповідають значенням 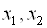, При яких відхилення 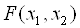від 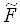буде мінімальним.

Таким чином, при даних значеннях вагових коефіцієнтів ми отримуємо наступні оптимальні (з точки зору досягнення оптимального значення "сукупної" функції 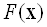) Значення компонент вектор функції:

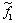
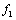
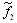
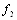
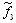
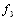
1,0748 0,7815 0,7358 0,3609 2 1,6784

З вищенаведеної таблиці видно, що в результаті оптимізації 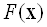значення всіх трьох функцій-складових зменшилися. Природно, при використанні інших вагових коефіцієнтів ми отримали б інші значення 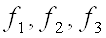(Але при будь-яких значеннях вагових коефіцієнтів тенденція зменшення всіх компонент вектор-функції зберігається).

Слід зазначити, що завдання цільового програмування може формулюватися дещо в інший спосіб. ЛПР може просто вказати, виходячи зі своїх міркувань, бажані з його точки зору, значення 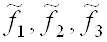, Або діапазони, в яких ці значення повинні бути локалізовані. При цій постановці завдання вирішується практично аналогічно, з тією відмінністю, що пошук оптимальних значень компонент (перша частина рішення) не проводиться, а їх значення (або діапазони зміни) вводяться в якості обмежень додатково до вихідних обмеженням завдання.